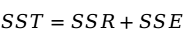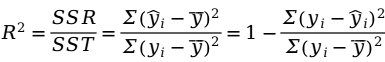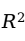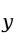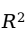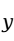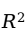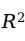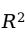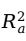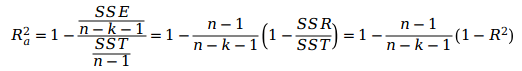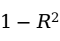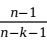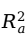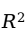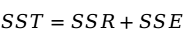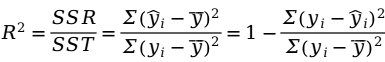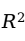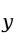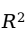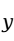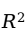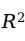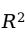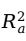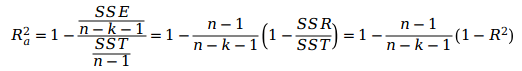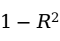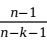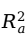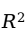多重判定系数
文章正文
发布时间:2024-09-11 13:02
跟一元回归分析中一样,在多元线性回归分析中离差平方和的分解也是一样的:
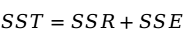
多重判定系数(multiple coefficient of determination)是多元线性回归平方和占总平方和的比例,计算公式为:
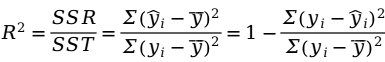
跟一元回归分析中的判定系数一样,多重判定系数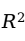
度量了多元线性回归方程的拟合程度,它可以解释为:在因变量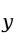
的总变差中被估计的多元线性回归方程所解释的比例。一般认为: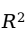
越大,回归模型的拟合效果越好。在多元线性回归分析中,模型中的解释变量越多,回归平方和SSR增大,残差平方和SSE减小,对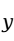
的变差的解释程度也就越高,则用上式计算的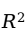
也就越大。即使增加一个与因变量无任何关系的随机变量作为解释变量,判定系数也会增大。如果单纯以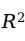
为目标模型评价标准,容易把不显著的自变量留在线性回归模型之中。因此在多元线性回归模型中一般需要对判定系数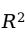
进行处理,计算调整后的多重判定系数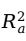
(adjusted multiple coefficient of determination):
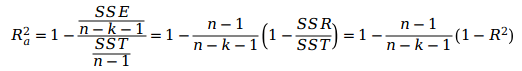
因为随着自变量个数k的增加,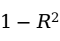
减少,但是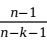
随着k的增加而增大,所以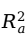
不一定随着自变量的增加而增大。我们可以直接利用统计软件得到其计算结果。
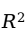
的平方根称为多重相关系数,也称为复相关系数,它度量了因变量同k个自变量的总体相关程度。
跟一元回归分析中一样,在多元线性回归分析中离差平方和的分解也是一样的:
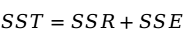
多重判定系数(multiple coefficient of determination)是多元线性回归平方和占总平方和的比例,计算公式为:
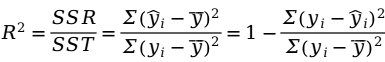
跟一元回归分析中的判定系数一样,多重判定系数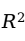
度量了多元线性回归方程的拟合程度,它可以解释为:在因变量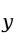
的总变差中被估计的多元线性回归方程所解释的比例。一般认为: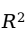
越大,回归模型的拟合效果越好。在多元线性回归分析中,模型中的解释变量越多,回归平方和SSR增大,残差平方和SSE减小,对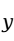
的变差的解释程度也就越高,则用上式计算的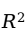
也就越大。即使增加一个与因变量无任何关系的随机变量作为解释变量,判定系数也会增大。如果单纯以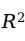
为目标模型评价标准,容易把不显著的自变量留在线性回归模型之中。因此在多元线性回归模型中一般需要对判定系数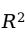
进行处理,计算调整后的多重判定系数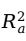
(adjusted multiple coefficient of determination):
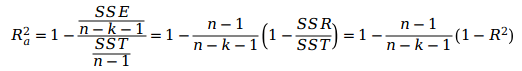
因为随着自变量个数k的增加,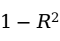
减少,但是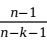
随着k的增加而增大,所以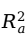
不一定随着自变量的增加而增大。我们可以直接利用统计软件得到其计算结果。
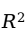
的平方根称为多重相关系数,也称为复相关系数,它度量了因变量同k个自变量的总体相关程度。